Présentation et définition
Le système de Hénon est un modèle proposé en 1976 par le mathématicien Michel Hénon. Ce modèle vise à rendre compte de certaines propriétés d’une section de Poincaré (définie plus loin) de l’attracteur de Lorenz. Il s’agit d’un système qui introduit des itérations dans le plan. Ces itérations sont définies par les relations suivantes.
 (3).
(3).
Dans cet exposé, on prendra pour conditions initiales (X0, Y0) = (1, 0), conditions initiales contenues dans le bassin d’attraction présenté plus loin. De plus, on prendra les valeurs suivantes: a = 1.4 et b = 0.3. Ces valeurs furent proposées par Michel Hénon et permettent d’observer un comportement chaotique.
Attracteur de Hénon
Alors, en très peu d’itérations, on considère que les points calculés sont sur l’attracteur. On obtient alors l’attracteur de Hénon.
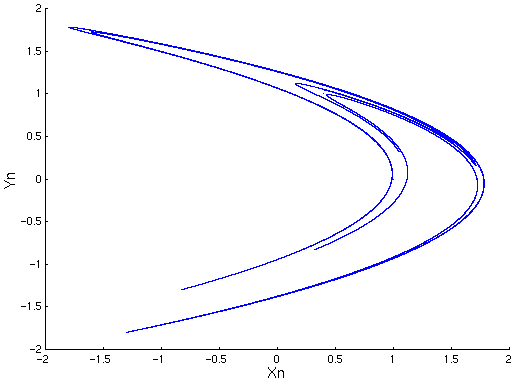
Bassin d’attraction
L’itération ne converge pas pour toutes les conditions initiales (X0, Y0). L’ensemble des conditions initiales telles que l’itération converge est le bassin d’attraction de l’attracteur. Un calcul numérique permet de construire une partie de ce bassin d’attraction.
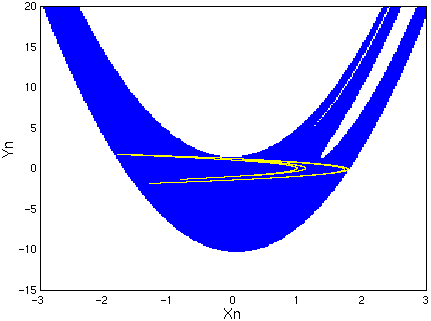
Influence du paramètre a – doublement de période
Le paramètre a revêt une importance particulière. Pour certaines valeurs de ce paramètre, le système est chaotique, pour d’autres, il ne l’est pas. En étudiant l’influence de a sur le caractère chaotique ou non du système, on met en évidence un phénomène caractéristique des systèmes chaotiques: le doublement de période.
Dans le cas général, le doublement de période se traduit par le doublement du nombre de trajectoires observée dans l’espace des phases. Dans notre cas, il implique un doublement du nombre de points limites de l’attracteur.
Avec (1, 0) pour conditions initiales, on constate les résultats suivants:
- – si -0.1225<a<0.3675, les itérations convergent vers un point du plan,
- – si 0.3675<a<0.9, les itérations tendent à constituer un suite (Xn, Yn) telle que (X2n, Y2n) converge vers un point et (X2n+1, Y2n+1) converge vers un autre point. On a donc deux points limites: on observe un doublement de période.
- – si 0.9<a<1.02, on assiste à un nouveau doublement de période.
Les doublements de période sont ensuite observés de plus en plus fréquemment à mesure qua a augmente. Pour rendre compte de ceci, on trace un diagramme de bifurcation. On indique la première coordonnée Xn des points limites en fonction de a. On y lit les valeurs limites de a indiquées précédemment.
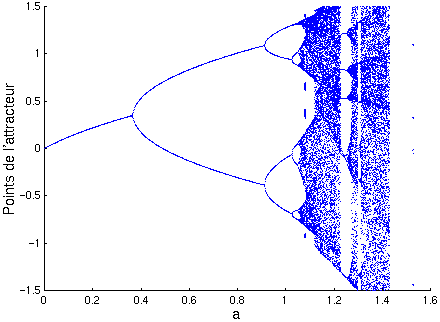
Pour a=1.4, on ne “distingue” plus les cycles (les points limites); le système présente un caractère chaotique.
Caractère chaotique
Pour caractériser un système chaotiques, nous avons vu qu’il faut faire appel à l’exposant de Lyapunov.
Pour estimer l’exposant de Lyapunov, on a recours à une simulation numérique simple. On laisse évoluer le système à partir de deux conditions initiales différentes mais très proches. On obtient ainsi deux évolutions différentes et même très différentes à terme car le système est chaotique (donc, sensible aux conditions initiales).
L’exposant de Lyapunov rend compte de l’évolution de la distance euclidienne entre les deux évolutions (induites par des conditions initiales différentes).
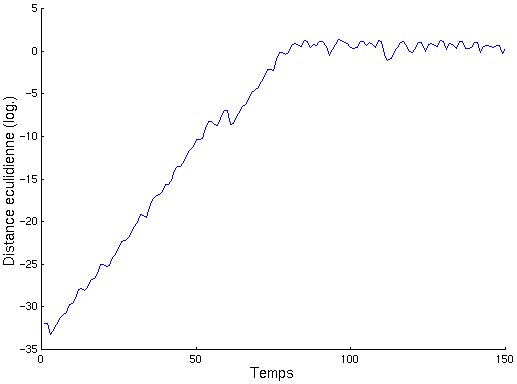
Le tracé en échelle logarithmique montre bien que la distance croit de manière exponentielle – du fait de la sensibilité aux conditions initiales. On peut lire la valeur de la pente (on peut aussi facilement utiliser une régression linéraire, mais cela ne se justifie pas ici) qui est la valeur de l’exposant de Lyapunov. Ici, on trouve un exposant de Lyapunov d’une valeur de 0.46.
Le palier observé à partir de 80 itérations environ mérite un commentaire. Il est dû à la taille de l’attracteur qui est limitée dans le plan.