Pour contrôler les attracteurs de Lorenz et Rössler, on utilise la méthode OGY, qui se trouve simplifiée du fait de la structure des sections de Poincaré impliquées. En effet, les attracteurs possèdent des dimensions de Hausdorff proche de 2 (environ 2.06 pour Lorenz). Ainsi, les sections de Poincaré sont de simples courbes.
Section de Poincaré
On rappelle la forme du système de Rössler:
 (8).
(8).
La section de Poincaré considérée ici est assez simple car elle est l’ensemble des points de l’attracteur tels que X = Xmax.
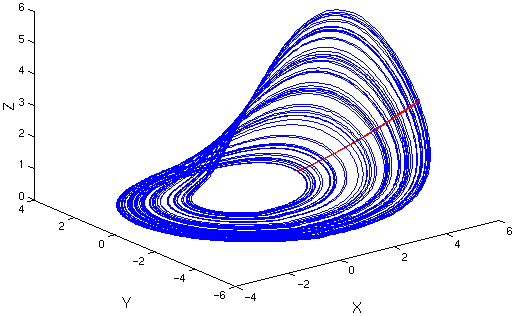
Application de premier retour
On s’intéresse à l’application de premier retour par rapport à la première coordonnée.
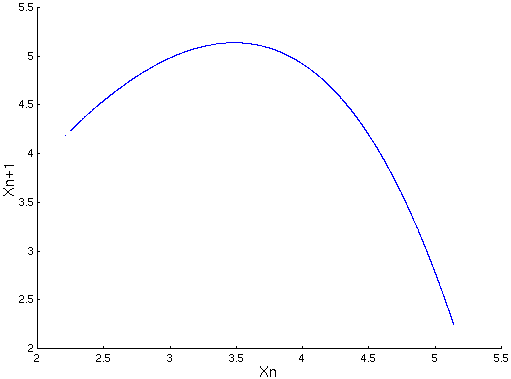
On constate que cette courbe est particulièrement simple, c’est la raison pour laquelle on utilise la méthode OGY simplifiée.
Point fixe
Le contrôle se fait au voisinage du point fixe, il est donc nécessaire de le déterminer.
Vu la structure de l’attracteur, trouver la valeur de la première coordonnée du point fixe permet de déterminer le point fixe dans la section de Poincaré. On utilise donc l’application de premier retour par rapport à la première coordonnée.
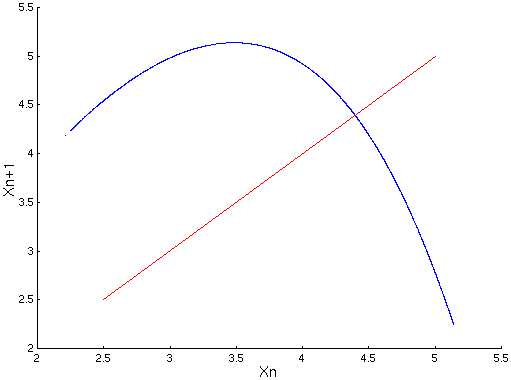
Calcul des perturbations
La méthode OGY nécessite de déterminer les directions et valeurs propres de la matrice jacobienne A. Ici, les sections de Poincaré sont assimilables à des courbes: on ne s’intéresse qu’à une seule direction propre et on obtient directement la correction.
On détermine pour cela l’influence du paramètre de contrôle, a pour le système de Rössler, sur le point fixe. Pour plusieurs valeurs du paramètre, on recherche le point fixe, tout comme dans le cas de l’attracteur de Lorenz.. On génère alors plusieurs applications de premier retour.
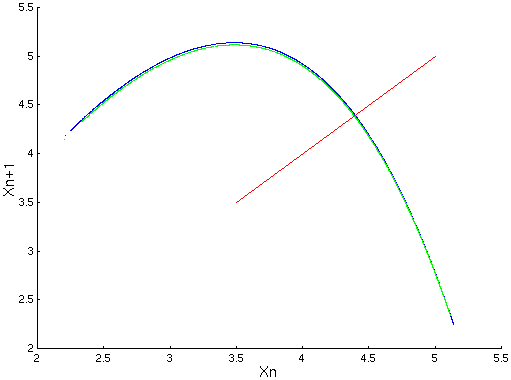
Connaissant l’influence du paramètre sur le point fixe et, par extension, sur les points au voisinage du point fixe, on est en mesure de déterminer quelle variation du paramètre doit être appliquée pour ramener, dans la section de Poincaré et au prochain passage, le point courant au point fixe. On obtient la loi de contrôle:
