Présentation
Proposé par l’Allemand Otto Rössler, le système de Rössler est lié à l’étude de l’écoulement des fluides; il découle des équations de Navier-Stokes. Les équations de ce système ont été découvertes à la suite de travaux en cinétique chimique.
Equations
Les équations de ce système sont les suivantes:
 (8).
(8).
Les dérivées des premiers membres sont des dérivées partielles par rapport au temps.
a, b et c sont des contantes réelles. Sauf précisions contraires, on prendra désormais: a = 0.398, b = 2 et c = 4. On est alors en présence d’un système chaotique.
Evolution dans le temps
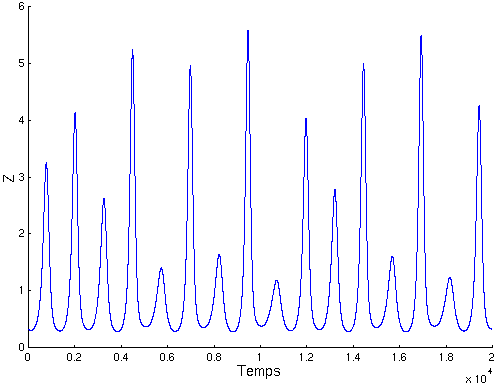
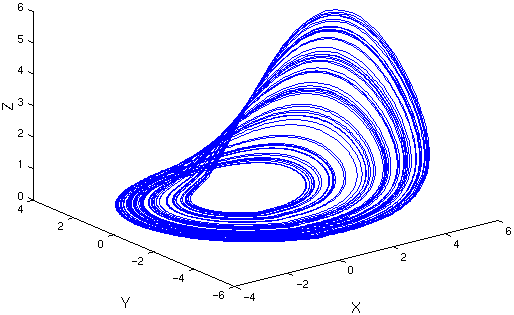
Attracteur de Rössler
Tout comme pour les attracteurs précédents, on génère l’espace des phases.
Doublement de période
Tout comme dans le cas de l’attracteur de Hénon, on peut constater un doublement de période si on fait évoluer le paramètre a. Lors de son évolution vers l’état chaotique (lorsque a augmente), on peut mettre en évidence une, puis deux, puis quatre… cycles dans l’espace des phases.
Exposant de Lyapunov
Considérant la définition de l’exposant de Lyapunov, on réalise les mêmes calculs que dans le cas de l’attracteur de Hénon.
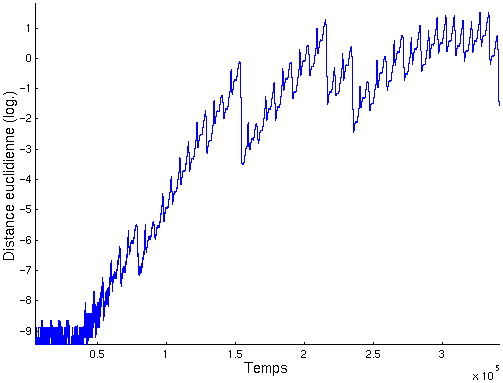
L’exposant de Lyapunov vaut ici 0.09.
Note: La première partie de la courbe (avant la croissance de la distance) ne traduit pas une croissance exponentielle. Le problème provient de l’enregistrement des données qui n’est pas assez précis pour qu’une distance euclidienne puisse être évaluée en-dessous de 10-9 (les calculs sont tout de même assez justes car c’est l’enregistrement des données qui est en cause ici, pas leur stockage en mémoire).