Problème
Lors du contrôle, on affecte le paramètre de contrôle. Il convient donc d’étudier son évolution au cours du temps. Il faut notamment vérifier qu’il ne varie pas trop rapidement et que les valeurs qu’il prend ne sont pas trop différentes de la valeur nominale (pour que le système conserve ses propriétés).
Cas de l’attracteur de Hénon
Au moment de l’application du contrôle, on constate que l’itération converge très rapidement vers le point fixe. La correction appliquée diminue donc très rapidement (elle dépend linérairement de la distance au point fixe). Si le contrôle est déclenché à une distance acceptable (voir, plus loin, distance de contrôle), une première correction de l’ordre de 10-2 est appliquée lorsqu’on passe une première fois à proximité du point fixe. Ensuite, le point courant de l’itération se rapprochant toujours plus du point fixe, la correction à appliquer est de plus en plus faible. La correction se stabilise enfin à une valeur très faible de 10-16.
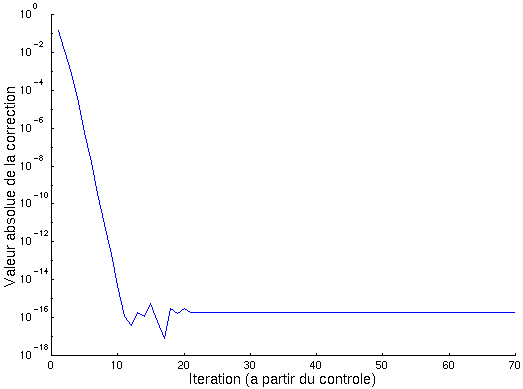
On peut considérer que les corrections ne sont pas très importantes et donc tout à fait acceptables.
Cas de l’attracteur de Lorenz
Dans le cas de l’attracteur de Lorenz, l’observation des résultats du contrôle nous amène aux mêmes conclusions: après une première correction, la correction appliquée à chaque itération est de plus en plus faible et le paramètre de contrôle se rapproche de sa valeur nominale, se stabilise autour d’une valeur proche et fluctue très faiblement autour de celle-ci. On observe ci-dessous l’évolution du paramètre de contrôle en fonction du temps. Cette évolution a un aspect de décroissance exponentielle.
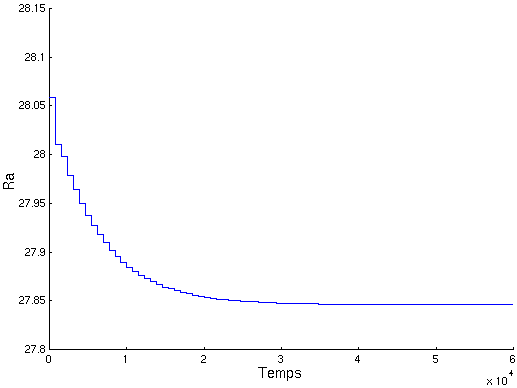
n général, l’évolution est légèrement différente mais reste assez semblable. Dans le cas général, on constate quelques corrections assez importantes (mais raisonnables). Ensuite, on constate bien une évolution exponentielle, croissante ou décroissante. Enfin, le paramètre se stabilise autour d’une valeur qui n’a aucune raison d’être la valeur nominale. La valeur stabilisée n’est pas très éloignée de la valeur initiale, sauf si on commet des erreurs sensibles dans l’estimation du point fixe et dans les calculs des perturbations. L’évolution du paramètre est donc pleinement satisfaisante.
Cas de l’attracteur de Rössler
Dans le cas de l’attracteur de Rössler, on constate que le paramètre de contrôle subit quelques variations plus importantes que les autres, puis oscille autour d’une valeur de référence, qui n’est pas nécessairement la valeur nominale imposée avant le contrôle (en ceci la courbe suivante est un cas particulier).
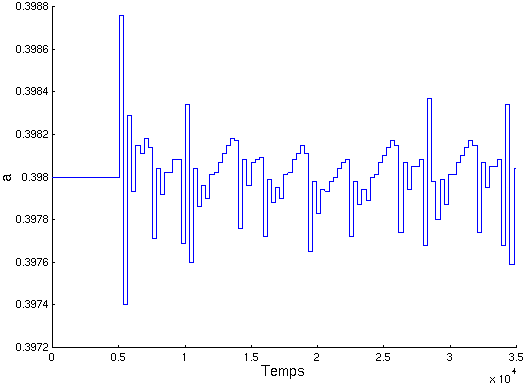
La différence fondamentale avec l’attracteur de Lorenz est l’absence d’évolution exponentielle. On note aussi que les oscillations sont plus importantes dans la dernière phase d’évolution que dans le cas de l’attracteur de Lorenz. Néanmoins, l’évolution est encore satisfaisante.